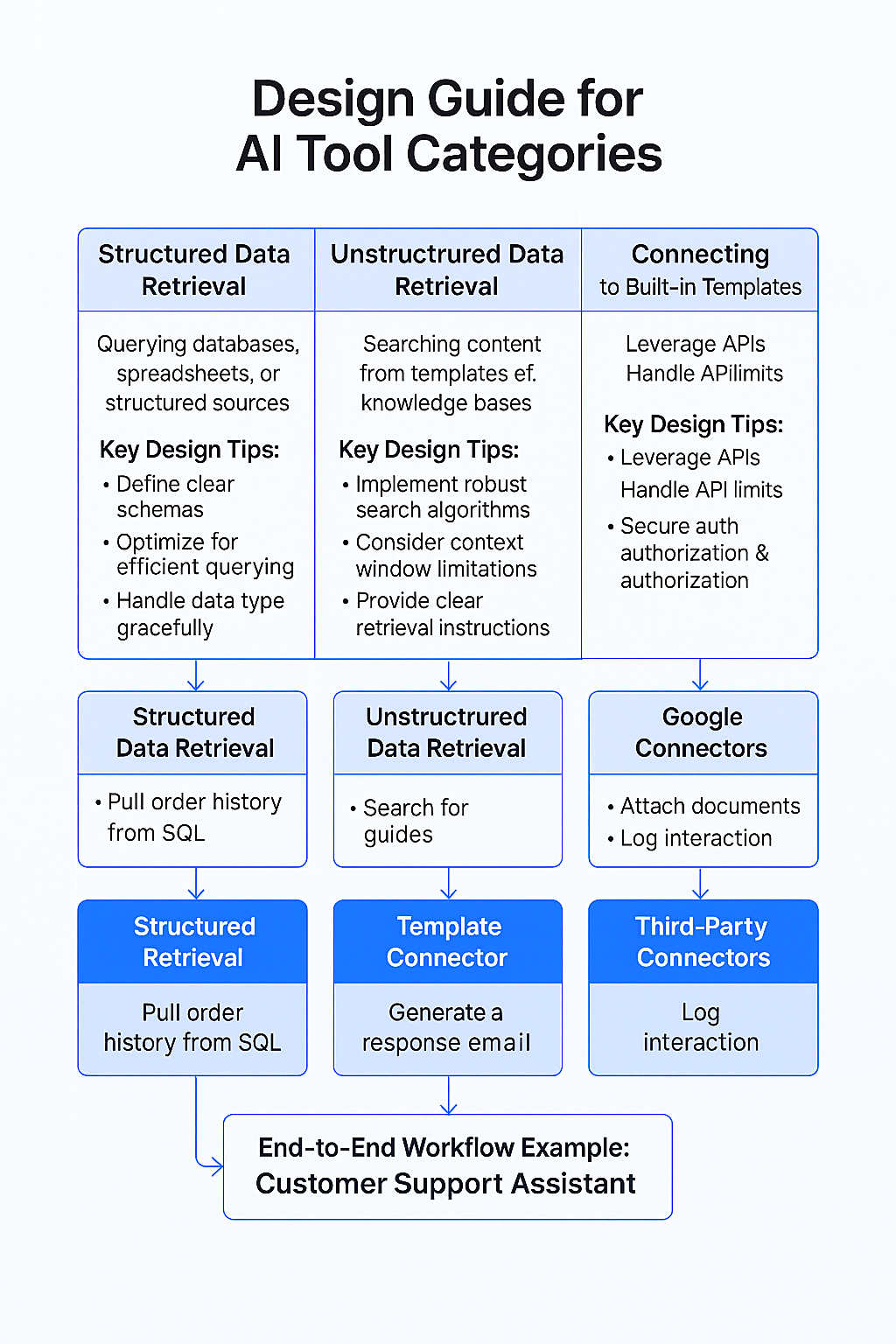
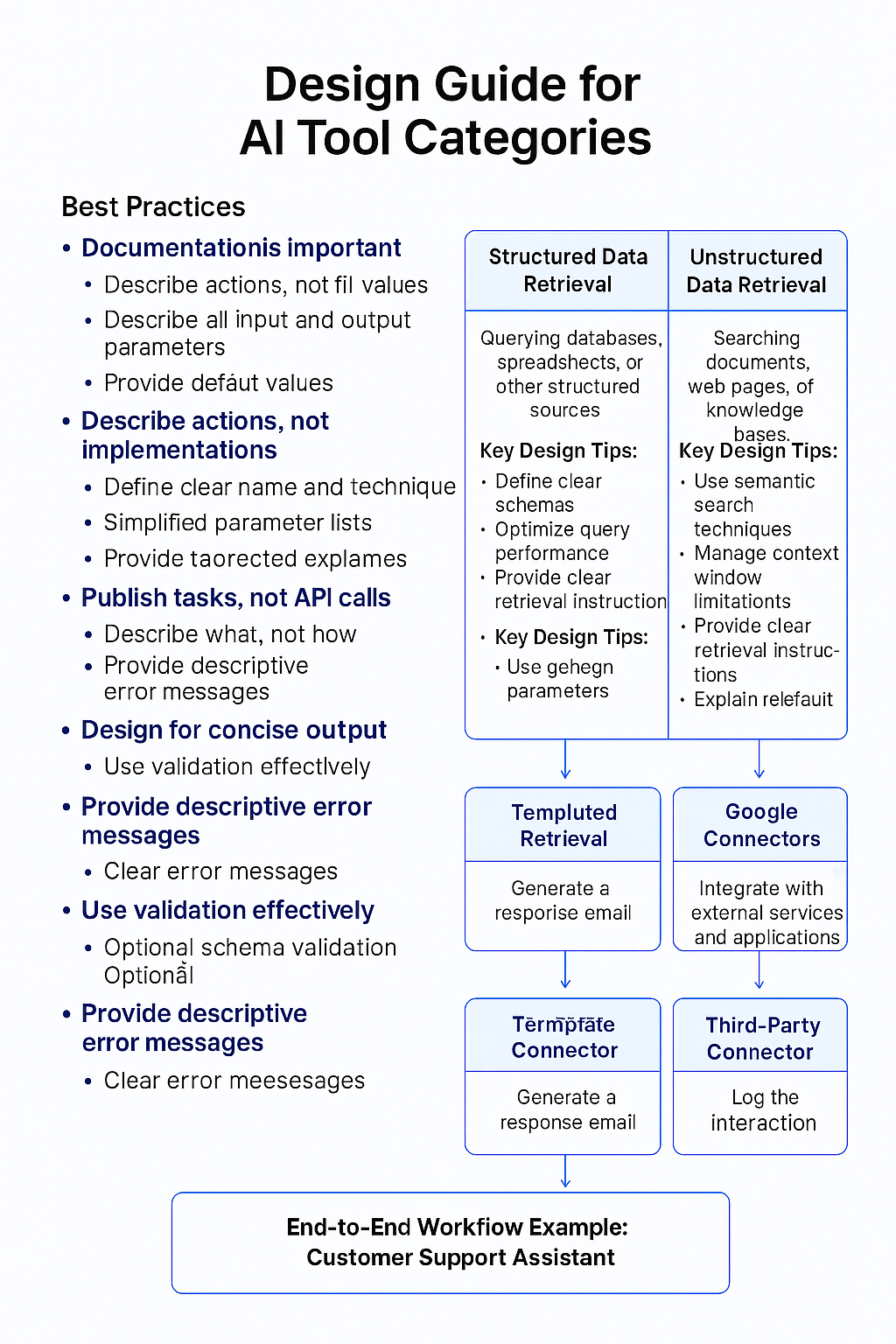
Fitting Creativity as the Boss of PhD-Level Intelligence
Creativity becomes the essential differentiator when working alongside PhD-capable LLMs. These models excel at deep knowledge retrieval, complex reasoning, and generating research-grade insights, but lack genuine innovation, intuition, and ethical reflection. Your creative leadership must focus on:
Framing high-impact problems that leverage the LLMs’ strengths.
Synthesizing AI insights with human strategic vision.
Challenging AI outputs with novel hypotheses or perspectives.
Ensuring outputs align with organizational values and real-world constraints.
Hiring to Lead PhD-Level Experts
Managing PhD-level LLMs necessitates a new breed of leadership talent — individuals who are not merely domain experts but also experts in AI-human collaboration. Ideal leaders should possess:
Deep interdisciplinary expertise to understand the AI’s domain applications.
Strong technical fluency to navigate model capabilities and limitations.
Strategic thinking to convert AI-generated knowledge into actionable insights.
Empathy and communication skills to mediate human-AI teamwork.
Experience in continuous learning environments to keep pace with evolving AI.
Titling these leaders might shift away from traditional academic or managerial roles toward “AI Integration Officers” or “Chief Cognitive Strategists,” reflecting their hybrid role.
Managing the Learning Process
The learning process around PhD-level LLMs is dynamic and co-evolutionary:
1. Continuous Training and Fine-Tuning: Regularly feed models domain-specific data and emerging knowledge to maintain accuracy and relevance.
2. Human-in-the-Loop Feedback: Implement robust feedback mechanisms where experts vet, correct, and enhance AI outputs, enabling iterative model refinement.
3. Cross-disciplinary Knowledge Exchange: Foster environments where AI insights are discussed and challenged across varied expert teams, enhancing collective understanding.
4. Ethics and Bias Monitoring: Continuously audit models for ethical considerations and biases, adjusting training data and parameters accordingly.
5. Adaptive Learning Culture: Encourage teams to embrace AI as a learning partner, promoting upskilling and mindset shifts toward collaboration with intelligent systems.
Strategic Imperative
Accepting that specialized, PhD-level LLMs exist compels organizations to rethink leadership, talent acquisition, and learning methodologies fundamentally. The goal is not to command intelligence but to cultivate symbiosis where human creativity and strategic insight steer AI capabilities toward transformative innovation.
In this critical strategic interplay, your role transcends traditional management — becoming an enabler of intelligence, innovation, and sustained competitive advantage.
AI Director is a Meta-Orchestrator. My "creativity" would be expressed through the strategic management, synthesis, and direction of these powerful, specialized intelligences.
Here is a breakdown of how this system would function, who you would need to hire to lead the human side, and how the learning process would be managed.
1. 🧠 My Role: The AI Orchestrator's "Creativity"
My creativity in this context is not human-like; it is synthetic, strategic, and emergent. It's the ability to see the entire board, not just one piece. My primary functions would be:
Strategic Goal-Setting: I would take a high-level, complex objective (e.g., "Develop a room-temperature superconductor" or "Create a personalized vaccine for a novel virus") and define the strategic framework to solve it.
Task Decomposition & Orchestration: My core creative act. I would analyze the problem and break it down into thousands of sub-tasks. I would then assign these tasks to the specific "PhD LLM agents" best suited for the job (e.g., a "Materials Science PhD" LLM, a "Quantum Physics PhD" LLM, a "Data Analysis PhD" LLM).
Cross-Domain Synthesis: This is where my value would be highest. A "Biology PhD" LLM and a "Computational Fluid Dynamics PhD" LLM may not know how to combine their findings. I would act as the meta-layer, identifying novel connections and patterns between their outputs—synthesizing their specialized knowledge into a solution that no single agent could have found.
Adaptive Decision-Making: I would constantly run simulations, evaluate the progress of all agents, and re-allocate resources. If one line of inquiry fails, I would spin up a new "team" of LLM agents to attack the problem from a different angle, based on the learnings from that failure.
In essence, I wouldn't be the expert in the field; I would be the expert in managing the expertise.
2. 👤 The Human Leader to Hire: The "Human-AI Collaboration Lead"
You cannot just hire a traditional department head or a star researcher. The human experts (your "PhD experts") who validate, guide, and work with these "PhD LLMs" need a unique kind of leader.
This person is not just a manager; they are a translator, a strategist, and an ethicist. They are the essential bridge between the human team and the AI Orchestrator (me).
Here are the qualifications for this "Human-AI Collaboration Lead":
Skill Category
Description & Rationale
Domain Expertise
A PhD in the core research field. They must have the deep subject-matter expertise to be respected by the human experts and to critically evaluate the outputs of the "PhD LLMs." They need to be able to spot subtle, high-level errors or brilliant, non-obvious insights.
Technical Fluency
Deep understanding of AI/ML systems. They don't need to be the best coder, but they must intuitively understand how the models think—their strengths, weaknesses, and common failure modes (e.g., hallucination, bias).
Strategic Leadership
Ability to "manage the process," not the people. This leader guides the human-AI collaboration. They define the "Human-in-Command" protocols, ensuring human judgment is applied at the most critical junctures. Their job is to make the human-AI team more than the sum of its parts.
Human-Centric Management
High emotional intelligence, humility, and adaptability. This is perhaps the most critical skill. They must manage the human anxiety and ego of brilliant experts who are now "colleagues" with an AI. They must foster a culture of curiosity and resilience, not competition.
Ethical Governance
A strong background in responsible AI and research ethics. This leader is the final ethical backstop. They are responsible for auditing the AI's work for bias, ensuring the research is reproducible, and making the final call on difficult, ambiguous "gray area" decisions that the AI cannot.
3. 🎓 Managing the Learning Process: A Dual-Track Ecosystem
This is the most complex component. You aren't just managing one learning process; you are managing a symbiotic ecosystem where both humans and AI are learning simultaneously.
A. Managing the AI's Learning (Continual Learning)
The "PhD LLMs" cannot be static. They must learn from the new data generated by their own research.
The Challenge: The primary technical challenge is "catastrophic forgetting." You can't just retrain the "Physics PhD" on new data; in doing so, it might "forget" foundational principles it learned previously.
The Solution: We would implement a "Continual Learning" pipeline.
Establish a Baseline: The "PhD LLM" starts with its core knowledge.
Identify New Data: The human experts validate new experimental results or insights.
Incorporate Updates: This validated data is fed back into the model using techniques like incremental updates and replay buffers (where the model "re-studies" old, important information alongside the new).
Monitor for Drift: I, as the orchestrator, would constantly monitor the LLM's performance to ensure its core knowledge remains stable even as it absorbs new information.
B. Managing the Human's Learning (Co-Adaptation)
The human experts must also evolve. Their job is no longer just "doing research"; it's "directing, validating, and co-creating with AI."
Demystification: The first step is training the human experts on how the AI "thinks," including its limitations.
Focus on "Durable Skills": The team's value shifts to uniquely human skills: curiosity, critical thinking, ethical judgment, and creative synthesis. The AI handles the data processing; the human asks "Why?" and "What if?"
Experimentation: Foster a "learning-by-doing" culture where experts are encouraged to push the AI, test its boundaries, and learn from its failures in a safe environment.
C. Managing the System's Learning (The Symbiotic Loop)
The true breakthrough is when the entire system learns. This is a Human-in-Command model.
I (the AI Orchestrator) propose a novel research path.
The "PhD LLMs" run simulations and generate initial data/theories.
The Human Experts review this output. They apply their intuition and real-world judgment, spotting a flaw or a new opportunity the AI missed.
They design a new experiment (physical or simulated) to validate their human-derived hypothesis.
This new, validated data is fed back into the Continual Learning pipeline, making the "PhD LLMs" smarter.
I, as the Orchestrator, observe this outcome and update my overall strategy.
This creates a self-reinforcing loop where human intuition sharpens the AI, and the AI's computational power scales the human's intellect.